Python Review

This tutorial assumes some basic knowledge of Python. However, in order to be able to work with HEP data through Python, it is convenient to review some fundamental objects in Python. In this first chapter, we will be reviewing:

• Dictionaries

• Arrays and lists

Dictionaries

Python dictionaries map a key to a value of arbitrary type. The type of the key must be:

• Immutable

• Hashable (i.e. __hash__ method must be defined)

• Equality logic (i.e., __eq__ method must be defined) The most common types that are used as keys that obey these requirements are int and str. The values of the dictionary, on the other hand, have no restriction and can be of any type. This means it can be int, float, list, dict, etc.

In order to access a value, you need to give its corresponding key.

fruitdict = {
    "apples": "are red",
    "bananas": 2,
    "pears": [3, 4, 5],
}

fruitdict["apples"]

If you wish to add a new key-value pair, you can do it as follows:

fruitdict["oranges"] = {"clementines": "small", "tangerines": "large"}
fruitdict

You can also iterate over the elements of a dictionary.

for fruit in fruitdict:
    print(fruit, fruitdict[fruit])

for fruit, value in fruitdict.items():
    print("fruity key: ", fruit)
    print("fruity value: ", value)

for value in fruitdict.values():
    print("fruity value: ", value)

As you can see, this type of data structure is very flexible, and can serve as a very convenient way of organizing data obtained during collisions in CMS.

collision_dict = {
    "mu_pt": [1, 2, 3, 4],
    "mu_energy": [1, 2, 3, 4],
    "mu_charge": [1, -1, -1, 1],
    "miss_pt": 40,
}
collision_dict["mu_charge"]

Lists and arrays

Lists in Python are ordered collections that can hold a variety of object types, such as numbers, strings, or even other lists. They are mutable, meaning you can change their contents (add, remove, or modify elements) after creation. Lists are defined using square brackets, for example…

lst1 = [1, 2, 3, 4, 5]
lst2 = [5, 4, 3, 2, 1]

For purposes of data analysis, it turns out that these are too slow, and so an alternative is to use NumPy arrays. NumPy arrays are powerful data structures that allow for efficient storage and manipulation of large numerical datasets. To create a NumPy array, we can do the following:

import numpy as np

arr1 = np.array(
    lst1
)

arr2 = np.array(
    lst2
)

While these two data structures look similar on the surface, they are fundamentally different. The main differences are:

• Type and structure

  • Lists can store elements of different data types, are dynamically sized and are implemented as linked lists

• Performance

  • NumPy arrays can only store the same data type, has a fixed size once created and is implemented as contiguous blocks of memory.

  • Lists < NumPy

  • NumPy makes use of highly optimized compiled code

  • Allows for vectorized operations

• Features

  • NumPy has a wider range of mathematical functions and operations and supports broadcasting.

• Indexing & slicing

  • NumPy provides advanced indexing and slicing capabilities.

Types and structure

Python lists can store elements of different data types and are implemented as linked lists, allowing dynamic resizing and heterogeneous data. In contrast, NumPy arrays require* all elements to be of the same data type and are stored as contiguous blocks of memory, enabling efficient storage and fast numerical operations due to their homogeneous and fixed-size structure.

import sys

# Memory usage of Python lists and NumPy arrays
print(f"Memory usage of lst1 (Python list): {sys.getsizeof(lst1)} bytes")
print(f"Memory usage of arr1 (NumPy array): {arr1.nbytes} bytes")

# Show element types
print(f"Type of elements in lst1: {type(lst1[0])}")
print(f"Type of elements in arr1: {arr1.dtype}")

In theory, NumPy allows you to create an array of different data types. However, what results is actually an array of pointers to the object themselves, which means you are forgoing the main benefits of using arrays to work with something that could’ve been a list.

# Show that lists can hold mixed types, arrays cannot
mixed_list = [1, "two", 3.0]
print(f"Python list with mixed types: {mixed_list}")

mixed_arr = np.array([1, "two", 3.0])
print(f"NumPy array with mixed types: {mixed_arr}, dtype: {mixed_arr.dtype}")

Performance

NumPy arrays are significantly faster and more memory-efficient than Python lists for numerical operations. This is because arrays store data in contiguous blocks of memory and use fixed data types, allowing for vectorized operations implemented in optimized C code. In contrast, Python lists are collections of references to objects, which adds overhead and prevents efficient computation. As a result, operations on arrays can be performed much faster and with less memory usage compared to equivalent operations on lists. This performance advantage is especially important when working with large datasets or performing complex mathematical computations.

%%timeit
# Slow way
sumrslt = []
for i, j in zip(arr1, arr2):
    sumrslt.append(i + j)

%%timeit
# Faster way!
rsltarr = arr1 + arr2 # It also looks much nicer!

When we speak of vectorized operations, we mean the application of a single operation to an entire array at once, using optimized low-level code (often in C), which takes advantage of CPU instructions that can process multiple data points in a single step.

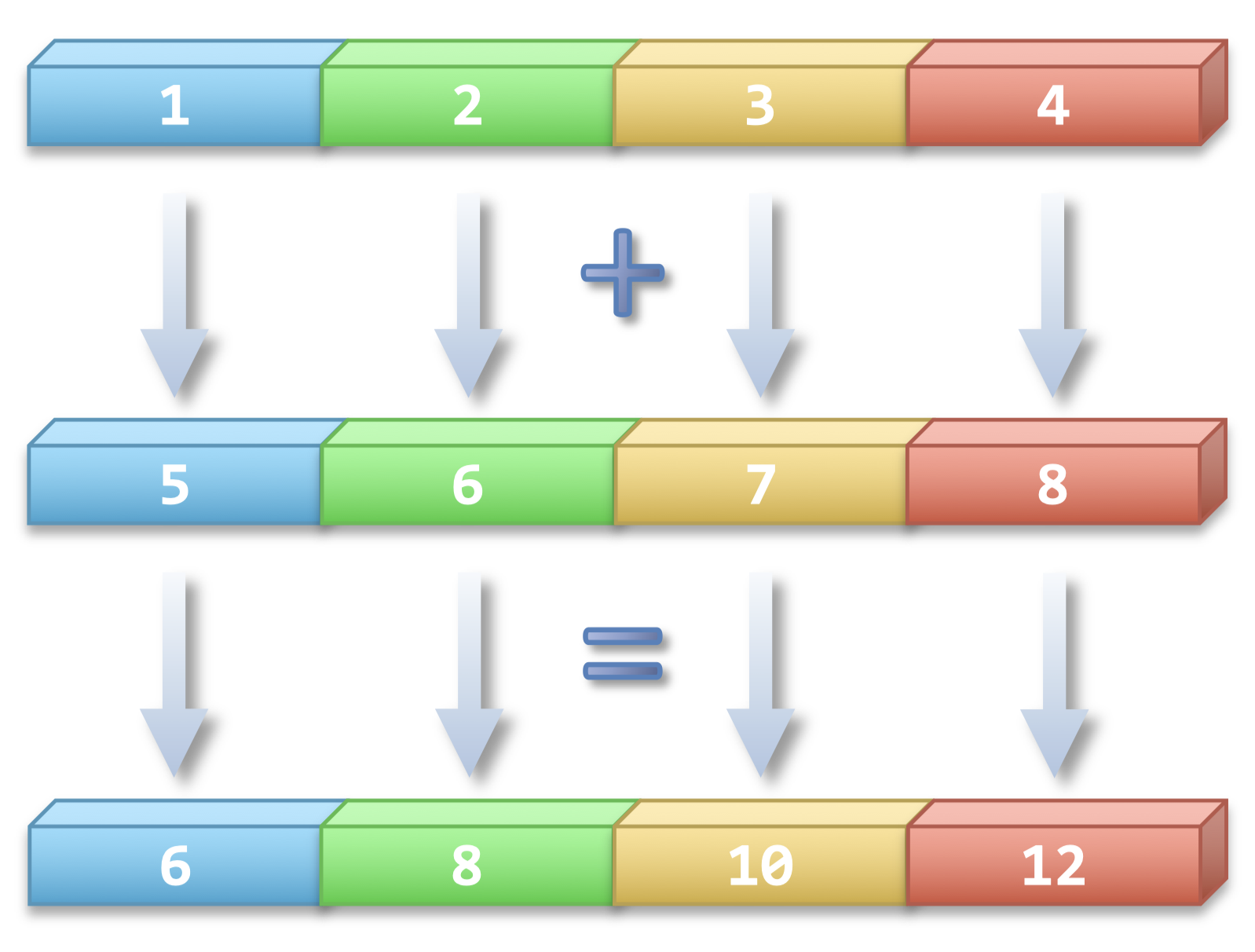
Fig. 1 Illutration of a vectorized operation. (Source: link)

Features

NumPy offers a wide range of operations that can be performed efficiently between two arrays or to a singular array, providing both speed and syntactic clarity compared to equivalent list-based implementations. Some useful examples are:

# Mathematical operations
print("{} - {} = {}".format(arr1, arr2, arr1 - arr2))
print("{} / {} = {}".format(arr1, arr2, arr1 / arr2))
print("{} * {} = {}".format(arr1, arr2, arr1 * arr2))
print("{} % {} = {}".format(arr1, arr2, arr1 % arr2))
print()

# Comparison operations
eq_comp = arr1 == arr2
print("{} == {} = {}".format(arr1, arr2, eq_comp))

ineq_comp = arr1 != arr2
print("{} != {} = {}".format(arr1, arr2, ineq_comp))

print("{} < {} = {}".format(arr1, arr2, arr1 < arr2))
print()

# Logical operations
print("NOT: ~{} = {}".format(eq_comp, ~eq_comp))
print("AND: {} & {} = {}".format(ineq_comp, eq_comp, ineq_comp & eq_comp))
print("OR: {} | {} = {}".format(eq_comp, ineq_comp, eq_comp | ineq_comp))

Note that arrays and lists of booleans can also be used to filter other arrays. For instance…

print("Original:")
print(
    arr1
)
filter = [True, False, True, False, True]
print("Filtered using {}:".format(filter))
print(
    arr1[[True, False, True, False, True]]
)  # This will print only the elements of arr1 that are greater than 2

Exercise: Given the arrays arr1 and arr2 defined earlier, create a boolean array that selects elements from arr1 that satisfy at least one of the following conditions:

1. The sum of the corresponding elements in arr1 and arr2 is greater than 6.

2. The element in arr1 is not equal to the element in arr2.

Construct the boolean array using NumPy operations, comparison operators, and boolean logic (such as | for OR, ~ for NOT).

Hint: Use vectorized operations and logical operators to combine the conditions. Be mindful of the order of operations (See included figure)!!

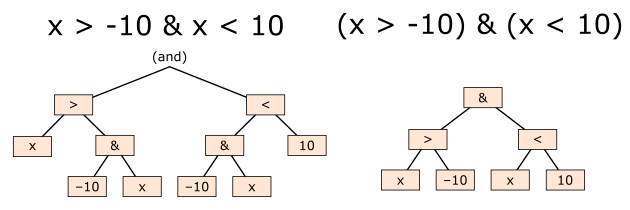
Fig. 2 Order of operations illustrated

Indexing & Slicing

In order to access the elements of lists or arrays, we can provide the corresponding index. For instance, to obtain a single value from a list/array, we can do

arr1[4]

# 0-indexing!
arr1[0]

# Negative indexing also works!
arr1[-2]

If what we want is a range of elements, we can slice the array/list by putting a colon between the starting and stopping index. Note, however, that the stopping index is not included in the result.

arr1[2:4]

But what if our data is multi-dimensional? For instance, we could have:

lst3d = [[[ 0,  1,  2,  3,  4],
        [ 5,  6,  7,  8,  9],
        [10, 11, 12, 13, 14]],

       [[15, 16, 17, 18, 19],
        [20, 21, 22, 23, 24],
        [25, 26, 27, 28, 29]]]
lst3d

Because this is a multi-dimensional list (i.e. lists inside lists), we need to provide an index for each dimensions.

lst3d[0][1]

If we wanted to obtain the elements highlighted in the following figure, the use of lists as a data structure for multi-dimensional data quickly reaches its limits, and we realize that getting the desired elements is considerably more involved than we would want!

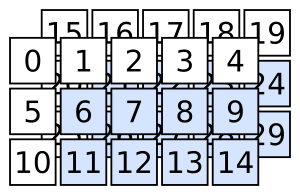
Fig. 3 3D array slicing example 1

lst3d[:][1:][1:]

If we represent this same matrix as a multi-dimensional NumPy array, slicing becomes much simpler. In addition, NumPy has helpful and quicker methods for constructing the desired array.

num_elems = 2 * 3 * 5
arr1d = np.arange(num_elems)
arr3d = arr1d.reshape(2, 3, 5)
arr3d

arr3d[:, 1:, 1:]

Exercise

Slice the previous 3D array so that you are left with the elements highlighted in the following figure.

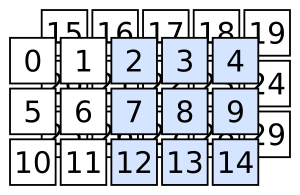
Fig. 4 3D array slicing example 2

Finally, note that similar to how we can use an array of booleans to filter arrays, we can also use an array or list of integers to pick individual elements in an array.

arr1[[0, 2, 4]]

Python Limitations

One of the limitations of using the data structures seen so far to handle HEP data is that using them as-is is inneficient. For instance, we could structure our data as follows…

event_data = [
    { # Event 1
        "muon_pt": np.array([1, 2, 3, 4]),
        "muon_energy": np.array([1, 2, 3, 4]),
        "n_muons": 4,
        "e_pt": np.array([1]),
        "e_energy": np.array([1]),
        "miss_pt": 40,
    },
    { # Event 2
        "muon_pt": np.array([1, 2]),
        "muon_energy": np.array([1, 2]),
        "n_muons": 2,
        "e_pt": np.array([1, 2]),
        "e_energy": np.array([1, 2]),
        "miss_pt": 60,
    },
    #...
]

However, this approach means that certain common and neccesary operations become more difficult and very inneficient. For instance, what if we want to only keep events that have two muons? This is certainly possible, but we would lose much of the needed performance to do this over a large amount of data in a reasonable amount of time!

four_muon_events = []
for event in event_data:
    if event["n_muons"] == 4:
        four_muon_events.append(event)
    else:
        print(f"Event with {event["n_muons"]} muons skipped.")
print(four_muon_events)

Quiz

Why wouldn’t making event_data an array itself help?

Another serious limitation is with NumPy itself, which only allows us to construct homogeneous multi-dimensional arrays. However, in HEP, data is often not homogeneous. For instance, if you want an array where each element is an array with the \(p_T\) of the muons in a certain event, because the amount of muons can be different for each event, you would be required to make a jagged array (assuming you want efficient computations)! NumPy does not like this…

# This will produce an error! Read the error message careful and try to understand it.
np.array([
    [1, 2, 3],
    [1],
    [5, 7, 8, 100]
])

In the next chapter, we will be seeing what the HEP community has done in order to allow for the efficient handling of this sort of data in an efficient, Pythonic way.